Soal dan Pembahasan SBMPTN Fisika 2021 (Kode )
Bimbel WIN:
Belajar dari bentuk soal yang sudah pernah ditanyakan membuat
persiapan menghadapi ujian yang sebenarnya akan menjadi lebih terarah,
lebih fokus dan lebih efektif.
Bentuk soal yang akan diujikan dari tahun ke tahun pada umumnya
materinya sama. Pada pelajaran yang menitikberatkan pada hafalan soanya bisa
sangat mirip bahkan ada yang persis sama. Sedangkan pada soal hitungan,
rumus dan analisanya pada umunya sama.
Oleh karena itu, kami menyarankan bagiadik-adik calon mahasiswa
baru (camaba) tahun ini, kuasailah minimal 10 tahun terakhir soal ujian yang
sudah pernah keluar.
💦 Soal no.1
Sebuah balok bermassa 2,0 kg bergerak pada sebuah bidang datar licin dengan kecepatan 1,0 m/s. selanjutnya, balok menuruni sebuah bidang miring dengan kemiringan \({\rm{3}}{{\rm{0}}^{\rm{o}}}\) dan mengalami gaya gesek sebesar 7,0 N. setelah sampai di dasar bidang miring, balok meluncur pada bidang datar licin pada kecepatan 2,0 \(\frac{m}{s}\). jika percepatan gavitasi pada tempat tersebut 10 \(\frac{m}{{{s^2}}}\). Kedua bidang datar berbeda ketinggian…
(B) 0,2 m
(C) 0,3 m
(D) 0,4 m
(E) 0,5 m
Pembahasan :
Usaha dan Energi
w = \(\Sigma F\) = \(\Delta Ek\)
w sin \({30^o}\) s - \({f_k}\) s = \({\rm{E}}{{\rm{k}}_{\rm{2}}}{\rm{ - E}}{{\rm{k}}_{\rm{1}}}\)
( w sin \({30^o}\) - \({f_k}\)) s = \(\frac{1}{2}m\,(\,{V_2}^2\, - \,{V_1}^2\,)\)
3 s = s
s = 1 m
maka, sin \({30^o}\) = \(\frac{h}{s}\)
h = 0,5 m
Kunci jawaban : E
Seorang pendengar sebut saja O berada di tengah diantara dua sumber bunyi yaitu P dan Q yang berada pada suatu garis lurus sumbu x, P berada di sebelah kiri O dan Q berada disebelah kanan P. saat diam P dan Q menghasilkan bunyi yang sama yaitu sebesar f. jika kemudian P bergerak kekiri dengan kelajuan konstan sebesar 0,25 \({{\rm{V}}_{\rm{o}}}\) dan Q bergerak ke kanan dengan kelajuan q \({{\rm{V}}_{\rm{o}}}\). menurut O terjadi layangan bunyi sebesar \(\frac{2}{{15}}\) f, jika \({{\rm{V}}_{\rm{o}}}\) adalah cepat rambat bunyi di udara maka kecepatan Q sebesar…. Vo m/s
Pembahasan :
Frekuensi pelayangan :
\({f_{pel}}\)= \(\left| {{f_{OP}}\, - \,{f_{OQ}}} \right|\)
Efek Doppler :
\({f_{pel}}\) = \(\left( {\frac{{{V_o}\, + \,{V_O}}}{{{V_o}\, + \,{V_s}}}} \right)\,f\, - \,\left( {\frac{{{V_o}\, + \,{V_O}}}{{{V_o}\, + \,{V_s}}}} \right)\,f\)
\(\frac{2}{{15}}f\, = \,\left( {\frac{{{V_o}\, + \,0}}{{{V_o}\, + \,0,25{V_o}}}} \right)\,f\, - \,\left( {\frac{{{V_o}\, + \,0}}{{{V_o}\, + \,q{V_o}}}} \right)\,f\)
\(\frac{2}{{15}}\, = \,\left( {\frac{{{V_o}\, + \,0}}{{{V_o}\,\left( {1\, + \,0,25} \right)}}} \right)\,\, - \,\left( {\frac{{{V_o}\, + \,0}}{{{V_o}\,\left( {1\, + \,q} \right)}}} \right)\,\)
\(\frac{1}{{\left( {1\, + \,q} \right)}}\, = \,\frac{{10}}{{15}}\)
\(q = \,0,5\)
Kunci Jawaban : E
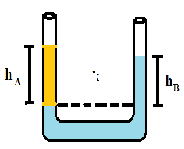
Sebuah bejana berhubungan pipa U diisi dua buah cairan dengan massa jenis yang berbeda yaitu A dan B. jika massa jenis cairan A adalah 1000 kali lipat dari massa jenis udara dan setengah kali dari massa jenis cairan B. saat ujung pipa terbuka B ditiup mendatar denga laju udara v menyebabkan ketinggian kolom cairan seperti gambar. Jika \({{\rm{h}}_{\rm{A}}}{\rm{ - 2 }}{{\rm{h}}_{\rm{B}}}\) = h cm. besar v sebesar…. \(\frac{m}{s}\)
(B) 200 \(\sqrt {( - 2h} )\)
(C) 100 \(\sqrt {( - 2h} )\)
(D) 200 \(\sqrt {( - h} )\)
(E) 10 \(\sqrt {( - 2h} )\)
Pembahasan :
Tekanan pd kedua ujung pipa :
Hk Bernoulli,
\({{\rm{P}}_{\rm{A}}}\)+\({\rho _u}\,g\,{h_A}\)+\(\frac{1}{2}\,{\rho _u}\,{v_A}^2\)=\({P_B}\) + \({\rho _u}\,g\,{h_B}\) + \(\frac{1}{2}\,{\rho _u}\,{v_B}^2\)
\(\left( {{h_A}\, = \,{h_B}} \right)\)
\({v_A}\, = \,0\)
\({v_B}\, = \,v\)
\({{\rm{P}}_{\rm{A}}}\) = \({P_B}\) + \(\frac{1}{2}\,{\rho _u}\,{v^2}\)
Tekanan pd bdang batas bawah zat cair :
\({{\rm{P}}_{\rm{A}}}\)+\({\rho _u}\,g\,{h_A}\)+\(\frac{1}{2}\,{\rho _u}\,{v_A}^2\)=\({P_B}\) + \({\rho _u}\,g\,{h_B}\) + \(\frac{1}{2}\,{\rho _u}\,{v_B}^2\)
\({v_A}\, = \,{v_B}\) = 0
substitusi pers. 1 dan \({\rho _u}\)
\({P_B}\)+ \(\frac{1}{2}\,{\rho _u}\,{v^2}\) + 10.000 \({h_A}\) = \({P_B}\) + 20.000 \({h_B}\)
\({v^2}\) = 40.000 \({h_B}\) - 20.000 \({h_A}\)
v = \(\sqrt {20000(2{h_B}\, - {h_A})} \)
\(2{h_B}\, - {h_A}\, = \, - h\)
v = \(100\,\sqrt {\left( { - 2h} \right)} \)
Kunci jawaban : C
Gas ideal diatomik sebanyak n mol mengalami poses termodinamika pada tekanan tetap b Pa dari keadaan 1 ke keadaan 2, dengan volume \({{\rm{V}}_{\rm{1}}}\) = a \({{\rm{m}}^{\rm{3}}}\) dan \({{\rm{V}}_{\rm{2}}}\) = 4 \({{\rm{V}}_{\rm{1}}}\). dalam proses tersebut, gas menyerap kalor sebesar .... J
(B) 11 ab
(C) 11,5 ab
(D) 12 ab
(E) 12,5 ab
Pembahasan :
Usaha (w) : Isobarik
\(W = P\left(
{{V_2} - {V_1}} \right)\)
W = b (4a – a)
W = 3 ab 2
Perubahan energy dalam \(\left( {\Delta V} \right)\) =
\(\Delta V
= \frac{5}{2}nR\Delta T = \frac{5}{2}p\left( {{V_2} - {V_1}} \right)\)
\(\Delta V =
\frac{5}{2}3 \cdot a \cdot b\)
= 7,5 ab 2
Hk I Thermodinamika :
\(Q = W +
\Delta V\)
= 3 ab + 7,5 ab
Q = 10,5 ab
Kunci jawaban : A
Sebuah bandul matematis sederhana dipasang pada langit langit kabin sebuah wahana ruang angkasa. Panjang tali bandul adalah 1 m. pada suatu saat wahana sedang jatuh dari benda angkasa apapun dan dipercepat searah dengan vektor normal pada lantai kabin. jika waktu itu bandul diayun dengan frekuensi 0,48 Hz. Jika tali bandul diganti dengan tali lain dengan panjang 2,25 m. Frekuensi bandul itu setelah diganti adalah...
(B) 0,42
(C) 0,54
(D) 0,68
(E) 0,74
Pembahasan :
Frekuensi ayunan bandul
\(\frac{{{f_1}}}{{{f_2}}}
= \frac{{\sqrt {{\ell _2}} }}{{\sqrt {{\ell _1}} }}\)
\(\frac{{0,48}}{{{f_2}}}
= \frac{{\sqrt {2,25} }}{{\sqrt 1 }} = \frac{{h5}}{1}\)
F2 = 0,32 Hz
Kunci jawaban : A
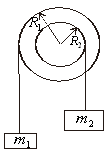
Suatu sistem mekanik tersusun dari dua katrol berbentuk silinder pejal yang di tempel sesumbu seperti pada gambar. Jari-jari \({{\rm{R}}_{\rm{1}}}\) =10 cm, dan \({{\rm{R}}_{\rm{2}}}\) = 5 cm. Pada setiap katrol dililitkan seutas tali dengan beban di ujungnya. Jika tegangan tali pada \({{\rm{m}}_{\rm{1}}}\) = 12,5 N dan pada \({{\rm{m}}_{\rm{2}}}\) = 15 N sedangkan percepatan linear beban m2 = 2,5 \({{\rm{m}}_{\rm{2}}}\) dan momen inersia katrol pertama 0,005 kg\({{\rm{m}}^{\rm{2}}}\), momen inersia katrol kedua adalah....kg\({{\rm{m}}^{\rm{2}}}\)
(B) 0,004
(C) 0,005
(D) 0,006
(E) 0,007
Pembahasan :
Dinamika rotasi :
\({ \propto
_1} = { \propto _2}\)
\(\frac{{{a_1}}}{{{R_1}}}
= \frac{{{a_2}}}{{{R_2}}}\)
Gerak rotasi :
\(\sum
{\sigma = I \cdot \propto } \)
\({T_1}
\times {R_1} - {T_2} \times {R_2} = \left( {{I_1} + {I_2}} \right)\frac{{{a_2}}}{{{R_2}}}\)
\(12,5\left(
{{{10}^{ - 1}}} \right) - 15\left( {5 \cdot {{10}^{ - 2}}} \right) = \left( {5
\cdot {{10}^{ - 3}} + {I_2}} \right)\frac{{2,5}}{{5 \cdot {{10}^{ - 2}}}}\)
\({I_2} = 5
\cdot {10^{ - 3}}{k_2}{m^2}\)
Kunci jawaban : C
Muatan titik A berada di x = 0 cm dan muatan titik B berada di x = 60 cm. sebuah muatan titik C diletakkan di titik x = 12 cm. jika muatan titik A 2 \(\mu \)C dan gaya listrik yang dialami muatan C sama dengan nol, muatan titik B sama dengan...\(\mu \)C.
(C) \(32\mu C\)
(D) \(53\mu C\)
(E) \(37\mu C\)
Pembahasan :
\({F_{CA}} =
{F_{CB}}\)
\(K\frac{{Qc
\cdot Q\Delta }}{{{{\left( {{r_{CA}}} \right)}^2}}} = k\frac{{{Q_C} \cdot
{Q_B}}}{{{{\left( {{r_{CB}}} \right)}^2}}}\)
\(\frac{2}{{{{\left(
{12} \right)}^2}}} = \frac{{{Q_B}}}{{{{\left( {48} \right)}^2}}}\)
\({Q_B} =
32\mu C\)
Kunci jawaban : C
Sebuah benda bergerak lurus dengan kecepatan tetap. Jika x dalam tabel di samping menunjukkan posisi benda tiap saat t, kecepatan benda tersebut adalah ... \(\frac{{\rm{m}}}{s}\).
(B) 1,5
(C) 2,5
(D) 5,0
(E) 7,5
Pembahasan :
Vttp => CLB
\(V =
\frac{{\Delta x}}{{\Delta t}} = \frac{{2,5 - 1}}{{1 - 0}} = \frac{{1,5}}{1} =
1,5{\raise0.7ex\hbox{$m$} \!\mathord{\left/
{\vphantom {m s}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{$s$}}\)
\(V =
\frac{{\Delta x}}{{\Delta t}} = \frac{{4 - 2,5}}{{2 - 1}} = \frac{{1,5}}{1} =
1,5{\raise0.7ex\hbox{$m$} \!\mathord{\left/
{\vphantom {m
s}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{$s$}}\)
Kunci jawaban : B
Dua balok bermassa \({{\rm{m}}_{\rm{1}}}\) = 1,0 kg dan \({{\rm{m}}_{\rm{2}}}\) = 2,0 kg saling terhubung dengan seutas tali yang bergerak tanpa slip melalui sebuah katrol dengan momen inersia 0,01 kg \({{\rm{m}}^{\rm{2}}}\). ]ika balok bergerak dengan percepatan linear 2,5 \(\frac{{\rm{m}}}{{{s^2}}}\) dan percepatan gravitasi 10 \(\frac{{\rm{m}}}{{{s^2}}}\), Jari-jari katrol adalah ... cm.
(C) 8,0
(D) 9,0
(E) 10,0
Pembahasan :
Benda I
\({T_1} -
{W_1} = {m_1} \cdot a\)
\({T_1} =
10 + 1\left( {2,5} \right)\)
\({T_1} =
12,5N\)
Benda 2
\({W_2} -
{T_2} = {M_2} \cdot a\)
\(T{ &
_2} = 20 - 2\left( {2,5} \right)\)
\({T_2} -
15N\)
\(\sum {\sigma = I \cdot
\propto } \)
\({T_2}
\cdot R - {T_1}R = I \cdot \frac{a}{R}\)
\(\left(
{{T_2} - {T_1}} \right){R^2} = I \cdot a\)
\(\left(
{15 - 12,5} \right){R^2} = {10^{ - 2}} \cdot 2,5\)
\(\cancel{{2,5}}{R^2}
= {10^{ - 2}} \cdot \cancel{{2,5}}\)
\(R = {10^{ -
1}}m \times {10^2} = {10^1}cm\)
Kunci jawaban : E
(B) 0,50
(C) 0,75
(D) 1,00
(E) 1,25
Pembahasan :
\(V = \frac{3}{5}C \to \gamma = \frac{5}{{\sqrt {{5^2} - {3^2}} }}\)
\(\gamma = \frac{5}{{\sqrt {25 - 9} }}\)
\(\gamma = \frac{5}{4}\)
P = m . V
=
\({m_o}
\cdot \frac{{\cancel{5}}}{4} \cdot \frac{3}{{\cancel{5}}}c\)
\(P = \frac{3}{4}{m_o}c
= 0,75{m_o}c\)
Kunci jawaban : C
Sebuah patikel bermassa \({{\rm{m}}_{\rm{o}}}\). Usaha yang diperlukan agar partikel tersebut memiliki energi total 1,5 \({{\rm{m}}_{\rm{o}}}{{\rm{c}}^{\rm{2}}}\) dari keadaan diam adalah .... \({{\rm{m}}_{\rm{o}}}{{\rm{c}}^{\rm{2}}}\)
(B) 1,25
(C) 1,00
(D) 0,75
(E) 0,5
Pembahasan :
\(E =
1,5{m_o}{c^2}\)
Energy kinetic:
\(Ek = E -
{E_o}\)
= \(m{c^2} - {m_o}{c^2}\)
= \({m_o}\gamma
{c^2} - {m_o}{c^2}\)
\(Ek =
{m_o}{c^2}\left( {\gamma - 1} \right)\)
\(Ek =
1,5{m_o}{c^2} - {m_o}{c^2}\)
\(Ek =
0,5{m_o}{c^2}\)
Usaha : \[W
= \Delta EK\)
\(W =
E{k_2} - E{k_1}\)
= 0,5 \[{m_o}{c^2}
- o\)
Sebuah bola pejal tenggelam ke dasar laut sehingga jari-jarinya berubah menjadi r akibat perubahan tekanan \(\Delta P\). Jika modulus bulk bola sebesar B, volume bola mula-mula adalah ....
(A) \(\frac{{{\rm{4\pi }}{{\rm{r}}^{\rm{3}}}}}{{{\rm{3(1 - }}\frac{{\rm{B}}}{{{\rm{\Delta P}}}}{\rm{)}}}}\)
(B) \(\frac{{{\rm{4\pi }}{{\rm{r}}^{\rm{3}}}}}{{{\rm{3(1 - }}\frac{{{\rm{\Delta P}}}}{{\rm{B}}}{\rm{)}}}}\)
(C) \(\frac{{{\rm{4\pi }}{{\rm{r}}^{\rm{3}}}{\rm{(1 - }}\frac{{\rm{B}}}{{{\rm{\Delta P}}}}{\rm{)}}}}{{\rm{3}}}\)
(D) \( - \frac{{{\rm{4\pi }}{{\rm{r}}^{\rm{3}}}{\rm{B}}}}{{3{\rm{\Delta P}}}}\)
(E) \( - \frac{{{\rm{4\pi }}{{\rm{r}}^{\rm{3}}}{\rm{\Delta P}}}}{{3{\rm{B}}}}\)
Pembahasan :
\(\Delta P =
\frac{{B \cdot \Delta v}}{{Vo}}\)
\(\Delta P
= \frac{{B\left( {Vo - Vt} \right)}}{{Vo}}\)
\(Vo =
\frac{{B\left( {Vo - \frac{4}{3}\pi {r^3}} \right)}}{{\Delta P}}\)
\(Vo \cdot
\Delta P = B \cdot Vo - \frac{4}{3}\pi {r^3} \cdot B\)
\(\Delta V
= {V_o} - V\)
\(\Delta V =
{V_o} - \frac{4}{3}\pi {r^3}\)
\(B \cdot
{V_o}\Delta P{V_o} = B \cdot \frac{4}{3}\pi {r^3}\)
\({V_o}\left(
{B - \Delta p} \right) = B \cdot \frac{4}{3}\pi {r^3}\)
\({V_o}\frac{{\frac{4}{3}\pi
{r^3}B}}{{B - \Delta P}} = \frac{{4\pi {r^3}B:B}}{{3\left( {\frac{B}{B} - \frac{{\Delta
P}}{B}} \right):B}}\)
\({V_o} =
\frac{{4\pi {r^3}}}{{3\left( {1 - \frac{{\Delta P}}{B}} \right)}}\)
Kunci jawaban : B
Pada percobaan efek fotolistrik diperoleh potensial penghenti \({{\rm{V}}_{{\rm{si}}}}\) untuk penyinaran dengan panjang gelombang 500 nm dan potensial penghenti 2,0 V untuk penyinaran dengan panjang gelombang 400 nm. Jika panjang gelobang ambang untuk logam target sama dengan 600 nm, nilai \({{\rm{V}}_{{\rm{si}}}}\) sama dengan .. V
(C) 0,6
(D) 0,5
(E) 0,2
Pembahasan :
\(V{s_2} =
\frac{{hc}}{q}\left( {\frac{1}{{400 \times {{10}^{ - 9}}}}\frac{1}{{600 \times
{{10}^{ - 9}}}}} \right)\)
\(2 =
\frac{{hc}}{{q \times {{10}^{ - 9}}}}\left( {\frac{{3 - 2}}{{1200}}} \right)\)
\(q =
\frac{{hc}}{{24 \cdot {{10}^{ - 7}}}}\)
\(V{s_1} =
\frac{{hc}}{q}\left( {\frac{1}{{500 \cdot {{10}^{ - 9}}}} - \frac{1}{{600 \cdot
{{10}^{ - 9}}}}} \right)\)
\(V{s_1} =
\frac{{hc}}{{{\raise0.7ex\hbox{${hc}$} \!\mathord{\left/
{\vphantom {{hc}
{24}}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{${24}$}}
\cdot {{10}^{ - 9}}}}\left( {\frac{{6 - 5}}{{3000 \cdot {{10}^{ - 9}}}}} \right)\)
= \(\frac{{24
\cdot {{10}^{ - 9}}}}{{{{10}^{ - 9}}}}\left( {\frac{{6 - 5}}{{3000}}} \right)\)
= \(V{s_1}
= \frac{{2400}}{{3000}}\)
\(V{s_1} =
0,8\,volt\)
Kunci jawaban : B
Pada suatu pecobaan efek fotolistik diperoleh nilai \(\frac{{hc}}{e}\) = 12,4 . \({\rm{1}}{{\rm{0}}^{{\rm{ - 7}}}}\) \(\frac{{jm}}{C}\) dengan h tetapan planck, c kelajuan cahaya dalam vakum dan e muatan elektron. Energi kinetik maksimum yang mungkin dimiliki elektron yang lepas sama dengan 1,03 eV. ketika percobaan dilakukan dengan foton berpanjang gelombang 400 nm. Panjang gelombang ambang untuk logam target sama dengan .... \(\eta {\rm{m}}\)
(C) 550
(D) 600
(E) 650
Pembahasan :
Vs = Vs
\(\frac{{Ek}}{e}
= \frac{{hc}}{e}\left( {\frac{1}{\lambda } - \frac{1}{{\lambda o}}} \right)\)
\(\frac{{Ek}}{e}
\times e = 12,4 \cdot {10^{ - 7}}\left( {\frac{1}{{4 \cdot {{10}^{ - 7}}}} - \frac{1}{{\lambda
o}}} \right)\)
\(1,03 =
12,4 \cdot {10^{ - 7}}\left( {\frac{1}{{4 \cdot {{10}^{ - 7}}}} - \frac{1}{{\lambda
o}}} \right)\)
\(\lambda o =
6 \cdot {10^{ - 7}}m\)
\(\lambda o = 600\eta m\)
Kunci jawaban : D
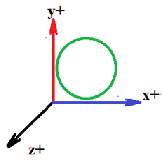
Proyeksi gerak sebuah partikel bermuatan negatif -q dan bermassa m pada bidang xy tampak pada gambar. Di ruang itu terrdapat medan magnetik tetap B searah sumbu z negatif, medan listrik tetap E searah sumbu z negatif, dan komponen kecepatan vz > 0. Komponen kecepatan pada bidang xy dan sifat vz adalah ....
(B) \(\frac{{qBR}}{m}\) berlawanan arah gerak jarum jam dan vz konstan
(C) \(\frac{{qBR}}{m}\) searah gerak jarum dan vz tidak konstan
(D) \(\frac{{qBR}}{m}\) searah gerak jarum jam dan vz konstan
(E) \(\frac{{qBm}}{R}\) spiral dan vz tidak konstan
Pembahasan :
Gaya Lorentz \(\left( {{F_L}} \right)\)
\(F = B
\cdot q \cdot V\,\,\sin \,\,\theta \)
\(\theta = 90^\circ
\to \) lintasan spiral
-
Untuk muatan 
:
Kaidah tangan kiri
Ibu jari : V
4 jari lain : B
Tapak tangan : \({F_L}\)
-
Arah gerak muatan searah gerak jarum jam
Gaya coulomb (Fc)
Fc = E . q
-
Oleh gaya coulomb muatan dipercepat searah sumbu
z